Two years ago, I wrote a post about THE universal language. Can you guess what language that is? Well, there are approximately six thousand-five hundred (6,500) spoken languages in the world today. However, approximately two thousand (2,000) of those languages have fewer than one thousand (1,000) speakers. The most popular language in the world is Mandarin Chinese. There are 1,213,000,000 people in the world speaking Mandarin. The following list will indicate the top ten (10) languages spoken.
- FRENCH: Number of speakers: 129 million
- MALAY-INDONESIAN: Number of speakers: 159 million
- PORTUGUESE: Number of speakers: 191 million
- BENGALI: Number of speakers: 211 million
- ARABIC: Number of speakers: 246 million
- RUSSIAN: Number of speakers: 277 million
- SPANISH: Number of speakers: 392 million
- HINDSTANI: Number of speakers: 497 million
- ENGLISH: Number of speakers: 508 million
- MANDARIN: Number of speakers: 1 billion+
An old-world language tree looks something like the following:
As you can see, language is very very complicated– but fascinating.
With this being the case, how on Earth could there be one UNIVERSAL language and what is it? MATHEMATICS is a language recognized and used by all people on our very small “blue dot”. I know this sounds very strange but that definitely is the case. So—do we celebrate accomplished mathematicians and if so how? YES, starting with the INTERNATIONAL MATHEMATICAL OLYMPAID (IM0) for pre-college. Let’s take a look.
IMO:
The International Mathematical Olympiad (IMO) is the World Championship Mathematics Competition for High School students and is held annually in a different country. The first IMO was held in 1959 in Romania, with 7 countries participating. It has gradually expanded to over 100 countries from 5 continents. The IMO Advisory Board ensures that the competition takes place each year and that each host country observes the regulations and traditions of the IMO. The IMO Foundation is a charity which supports the IMO. The IMO Foundation website is the public face of the IMO. This is a particularly valuable resource for people who are not necessarily mathematical specialists, but who want to understand the International Mathematical Olympiad.
The symbol for the IMO is given below.

ORIGIN:
The International Mathematical Olympiad (IMO) is an annual six-problem mathematical Olympiad for pre-college students, and is the oldest of the International Science Olympiads. Please note the phrase pre-college, although almost all of the students taking the test are high school age. This is due to the questions being asked. The first IMO was held in Romania in 1959. It has since been held annually, except for 1980. Approximately one hundred (100) countries send teams of up to six students, plus one team leader, one deputy leader, and observers to the Olympiad.
The content ranges from extremely difficult algebra and pre-calculus problems to problems involving branches of mathematics not conventionally covered at school nor university level, These are such problems as projective and complex geometry, functional equations and well-grounded number theory, of which extensive knowledge of theorems is required. Calculus, though allowed in solutions, is never required, as there is a principle that anyone with a basic understanding of mathematics should understand the problems, even if the solutions require a great deal more knowledge. Supporters of this principle claim that this allows more universality and creates an incentive to find elegant, deceptively simple-looking problems which nevertheless require a certain level of ingenuity.
The selection process differs by country, but it often consists of a series of tests which admit fewer students at each progressing test. Awards are given to approximately the top-scoring fifty percent (50%) of the individual contestants. Teams are not officially recognized—all scores are given only to individual contestants, but team scoring is unofficially compared more than individual scores. Contestants must be under the age of twenty (20) and must not be registered at any tertiary institution. Subject to these conditions, an individual may participate any number of times in the IMO.
SCORING AND FORMAT:
The examination consists of six problems. Each problem is worth seven points, so the maximum total score is forty-two (42) points. No calculators are allowed. The examination is held over two consecutive days; each day the contestants have four-and-a-half hours to solve three problems. The problems chosen are from various areas of secondary school mathematics, broadly classifiable as geometry, number theory, algebra, and combinatorics. They require no knowledge of higher mathematics such as calculus and analysis, and solutions are often short and elementary. However, they are usually disguised so as to make the solutions difficult. Prominently featured are algebraic inequalities, complex numbers, and construction-oriented geometrical problems, though in recent years the latter has not been as popular as before.
Each participating country, other than the host country, may submit suggested problems to a Problem Selection Committee provided by the host country, which reduces the submitted problems to a shortlist. The team leaders arrive at the IMO a few days in advance of the contestants and form the IMO Jury which is responsible for all the formal decisions relating to the contest, starting with selecting the six problems from the shortlist. The Jury aims to order the problems so that the order in increasing difficulty is Q1, Q4, Q2, Q5, Q3 and Q6. As the leaders know the problems in advance of the contestants, they are kept strictly separated and observed.
Each country’s marks are agreed between that country’s leader and deputy leader and coordinators provided by the host country (the leader of the team whose country submitted the problem in the case of the marks of the host country), subject to the decisions of the chief coordinator and ultimately a jury if any disputes cannot be resolved.
RECENT AND FUTURE IMOS:
The two-day event is truly global in nature with the following locations having been selected.
- The 51st IMO was held in Astana, Kazakhstan, July 2–15, 2010.
- The 52nd IMO ]was held in Amsterdam, Netherlands, July 13–24, 2011.
- The 53rd IMO was held in Mar del Plata, Argentina, July 4–16, 2012.
- The 54th IMO was held in Santa Marta, Colombia, July 18–28, 2013.
- The 55th IMO was held in Cape Town, South Africa, July 3–13, 2014.
- The 56th IMO was held in Chiang Mai, Thailandin 2015.
- The 57th IMO was held in Hong Kongin 2016.
- The 58th IMO will be held in Rio de Janeiro, Brazilin 2017.
- The 59th IMO will be held in Romaniain 2018.
- The 60th IMO will be held in UKin 2019.
- The 61st IMO will be held in Petersburg, Russiain 2020.
The only countries to have their entire team score perfectly in the IMO were the United States in 1994 (they were coached by Paul Zeitz); and Luxembourg, whose one-member team had a perfect score in 1981. The US’s success earned a mention in TIME Magazine. Hungary won IMO 1975 in an unorthodox way when none of the eight team members received a gold medal (five silver, three bronze). Second place team East Germany also did not have a single gold medal winner (four silver, four bronze).
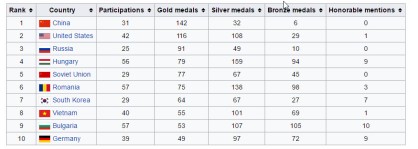
The top 10 countries with the best all-time results are as follows:
CONSLUSIONS:
I think a competition such as this is one of the best events sponsored because it gives recognition to those who excel within a specific discipline. After all, we have the Oscars, the Grammys, the People’s Choice Awards, the Country Music Awards. Pro Bowl, Super Bowl. Why not celebrate the talents of those around the world who “march to the beat of a different drummer”? Just a thought.



INTERNATIONAL MATHEMATICAL OLYMPIAD (IMO)
January 27, 2017
Two years ago, I wrote a post about THE universal language. Can you guess what language that is? Well, there are approximately six thousand-five hundred (6,500) spoken languages in the world today. However, approximately two thousand (2,000) of those languages have fewer than one thousand (1,000) speakers. The most popular language in the world is Mandarin Chinese. There are 1,213,000,000 people in the world speaking Mandarin. The following list will indicate the top ten (10) languages spoken.
An old-world language tree looks something like the following:
As you can see, language is very very complicated– but fascinating.
With this being the case, how on Earth could there be one UNIVERSAL language and what is it? MATHEMATICS is a language recognized and used by all people on our very small “blue dot”. I know this sounds very strange but that definitely is the case. So—do we celebrate accomplished mathematicians and if so how? YES, starting with the INTERNATIONAL MATHEMATICAL OLYMPAID (IM0) for pre-college. Let’s take a look.
IMO:
The International Mathematical Olympiad (IMO) is the World Championship Mathematics Competition for High School students and is held annually in a different country. The first IMO was held in 1959 in Romania, with 7 countries participating. It has gradually expanded to over 100 countries from 5 continents. The IMO Advisory Board ensures that the competition takes place each year and that each host country observes the regulations and traditions of the IMO. The IMO Foundation is a charity which supports the IMO. The IMO Foundation website is the public face of the IMO. This is a particularly valuable resource for people who are not necessarily mathematical specialists, but who want to understand the International Mathematical Olympiad.
The symbol for the IMO is given below.
ORIGIN:
The International Mathematical Olympiad (IMO) is an annual six-problem mathematical Olympiad for pre-college students, and is the oldest of the International Science Olympiads. Please note the phrase pre-college, although almost all of the students taking the test are high school age. This is due to the questions being asked. The first IMO was held in Romania in 1959. It has since been held annually, except for 1980. Approximately one hundred (100) countries send teams of up to six students, plus one team leader, one deputy leader, and observers to the Olympiad.
The content ranges from extremely difficult algebra and pre-calculus problems to problems involving branches of mathematics not conventionally covered at school nor university level, These are such problems as projective and complex geometry, functional equations and well-grounded number theory, of which extensive knowledge of theorems is required. Calculus, though allowed in solutions, is never required, as there is a principle that anyone with a basic understanding of mathematics should understand the problems, even if the solutions require a great deal more knowledge. Supporters of this principle claim that this allows more universality and creates an incentive to find elegant, deceptively simple-looking problems which nevertheless require a certain level of ingenuity.
The selection process differs by country, but it often consists of a series of tests which admit fewer students at each progressing test. Awards are given to approximately the top-scoring fifty percent (50%) of the individual contestants. Teams are not officially recognized—all scores are given only to individual contestants, but team scoring is unofficially compared more than individual scores. Contestants must be under the age of twenty (20) and must not be registered at any tertiary institution. Subject to these conditions, an individual may participate any number of times in the IMO.
SCORING AND FORMAT:
The examination consists of six problems. Each problem is worth seven points, so the maximum total score is forty-two (42) points. No calculators are allowed. The examination is held over two consecutive days; each day the contestants have four-and-a-half hours to solve three problems. The problems chosen are from various areas of secondary school mathematics, broadly classifiable as geometry, number theory, algebra, and combinatorics. They require no knowledge of higher mathematics such as calculus and analysis, and solutions are often short and elementary. However, they are usually disguised so as to make the solutions difficult. Prominently featured are algebraic inequalities, complex numbers, and construction-oriented geometrical problems, though in recent years the latter has not been as popular as before.
Each participating country, other than the host country, may submit suggested problems to a Problem Selection Committee provided by the host country, which reduces the submitted problems to a shortlist. The team leaders arrive at the IMO a few days in advance of the contestants and form the IMO Jury which is responsible for all the formal decisions relating to the contest, starting with selecting the six problems from the shortlist. The Jury aims to order the problems so that the order in increasing difficulty is Q1, Q4, Q2, Q5, Q3 and Q6. As the leaders know the problems in advance of the contestants, they are kept strictly separated and observed.
Each country’s marks are agreed between that country’s leader and deputy leader and coordinators provided by the host country (the leader of the team whose country submitted the problem in the case of the marks of the host country), subject to the decisions of the chief coordinator and ultimately a jury if any disputes cannot be resolved.
RECENT AND FUTURE IMOS:
The two-day event is truly global in nature with the following locations having been selected.
The only countries to have their entire team score perfectly in the IMO were the United States in 1994 (they were coached by Paul Zeitz); and Luxembourg, whose one-member team had a perfect score in 1981. The US’s success earned a mention in TIME Magazine. Hungary won IMO 1975 in an unorthodox way when none of the eight team members received a gold medal (five silver, three bronze). Second place team East Germany also did not have a single gold medal winner (four silver, four bronze).
The top 10 countries with the best all-time results are as follows:
CONSLUSIONS:
I think a competition such as this is one of the best events sponsored because it gives recognition to those who excel within a specific discipline. After all, we have the Oscars, the Grammys, the People’s Choice Awards, the Country Music Awards. Pro Bowl, Super Bowl. Why not celebrate the talents of those around the world who “march to the beat of a different drummer”? Just a thought.
Share this:
Tagged: Commentary, Education, Knowledge economy